1)約分
-
約分とは
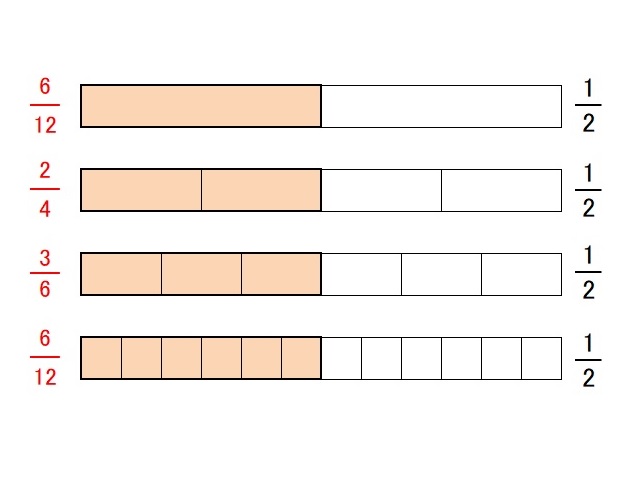
6/12,3/6,2/4,1/2は同じ大きさの分数、そこで6/12の分子と分母を同じ6(6と12の最大公約数)で割って1/2のような簡単な分数にする。このことを約分という。
-
画像
12を8で割ると余りが出る
12を7(8-1)で割ると余りが出る
12を6(8-2)で割ると余りが出る
12を5(8-3)で割ると余りが出る
12を4(8-4)で割ると割り切れる
よって、4が12と8の最大公約数である
12÷4=3 8÷4=2
したがって、2/3 -
プログラム
数②を数①で割ると余りが出る
数②を数①-1で割ると余りが出る
数②を数①-2で割ると余りが出る
数②を数①-3で割ると余りが出る
割り切れるまで繰り返す
最大公約数がGになったとすると
数①÷G / 数②÷G
2)通分
-
通分とは
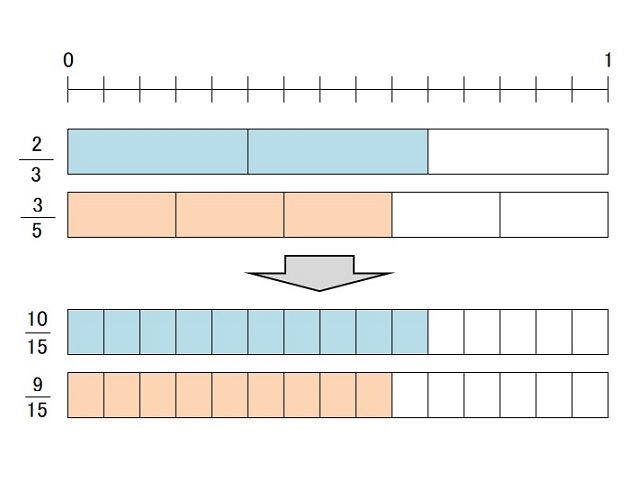
2/3と3/5のように分母が違う2つの分数について、分母15に(3と5の最小公倍数)にそろえることを通分という。
-
画像
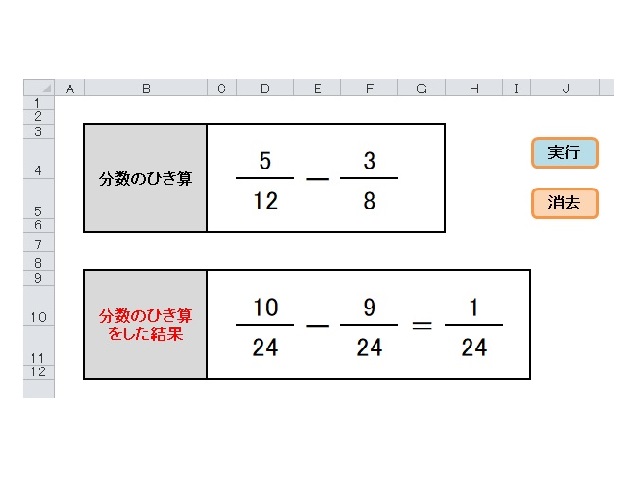
12を8で割ると余りが出る
12を7(8-1)で割ると余りが出る
12を6(8-2)で割ると余りが出る
12を5(8-3)で割ると余りが出る
12を4(8-4)で割ると割り切れる
よって、4が12と8の最大公約数である
分母は、8×12÷4=24
分子は、3×12÷4=9 と
5×18÷4=15 -
プログラム
数②を数①で割ると余りが出る
数②を数①-1で割ると余りが出る
数②を数①-2で割ると余りが出る
数②を数①-3で割ると余りが出る
割り切れるまで繰り返す
最大公約数がGになったとすると
分母は、分母1×分母2÷G
分子は、分子1×分母2÷G と
分子2×分母1÷G